Teste de Hipóteses aplicado à analise de projetos

O teste de χ² (Qui Quadrado) serve para estudar a dependência entre duas variáveis, verificando se a frequência absoluta observada é diferente da esperada.

Em outras palavras, ele checa se uma variável depende de outra para avaliar hipóteses como:

• A produtividade aumenta quando há menos gente num projeto?
• O desemprego varia junto com o câmbio do dólar?
• A lucratividade é maior em projetos menores?
• Os clientes compram mais se o preço é mais baixo?

Essas e outras infinitas hipóteses podem ser avaliadas através do teste de χ² (Qui Quadrado), basta possuir uma amostra do universo que se quer estudar, aplicar os cálculos (apenas uma fórmula no Excel) e analisar o resultado. Para seguir com o tutorial, sugiro baixar a planilha de exemplo. Vamos ao passo a passo!

Passo 1 – Tomar uma amostra de dados

Após definir o tamanho da amostra, juntam-se os dados em uma planilha comum. No exemplo a seguir, utilizei dados aleatórios de 12 projetos para listar informações sobre projetos de uma empresa.

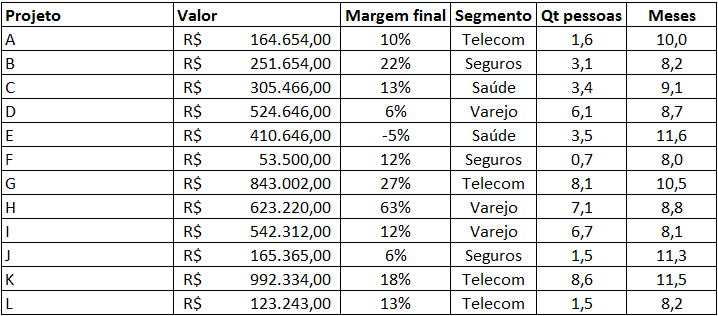
No mundo real: A quantidade deveria ser definida pelo tamanho da amostra e as colunas pelos dados necessários para realizar o teste de hipóteses.

Passo 2 – Organizar em dados nominais

Criei faixas para os valores de margem (Margem F), quantidade de pessoas (Qt F) e meses de projeto (Meses F). Essas faixas não seguiram nenhuma orientação especial, apenas a conveniência.

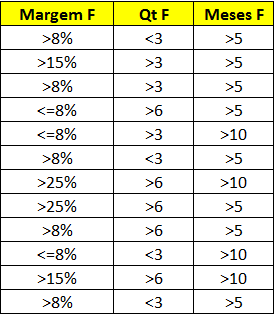
No mundo real: Devem-se construir faixas de frequência, por exemplo, utilizando a regra da raiz quadrada, que é: k = RAIZ(n). Ou seja, a raiz quadrada do tamanho da amostra (quantidade de itens) é igual ao número de faixas a utilizar. Se forem 350 itens, o k será igual a RAIZ(250) = 18,71, arrendondadas para 19 faixas.

Passo 3 – Construindo as hipóteses

Vencidos os dois primeiros passos, vamos à parte mais lógica, que é construir as hipóteses. Neste exemplo, construí 3 testes:

• Teste 1 – A margem bruta dos projetos é influenciada pelo segmento de negócio atendido?
• Teste 2 – A margem bruta dos projetos é influenciada pela quantidade de pessoas?
• Teste 3 – A margem bruta dos projetos é influenciada pela quantidade de meses de trabalho?

Bem, o teste de χ² (Qui Quadrado) vai responder se nesse conjunto de dados essas variáveis são dependentes ou independentes. Uma vez que descubra uma dependência, você poderá seguir a uma Análise de Correlação, mas isso é assunto para outro post.

Passo 4 – Organizando os dados no Excel

Dados reais

Para organizar os dados, deve-se construir uma Tabela Dinâmica no Excel a partir dos dados reais, como no exemplo abaixo.

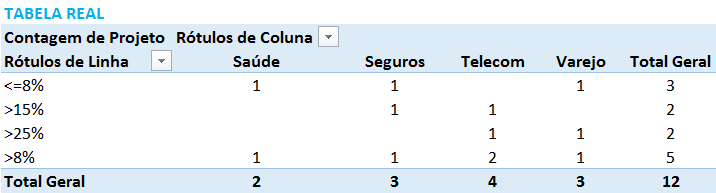
Observe que utilizei as faixas de “margem bruta” criadas no passo 2.

Dados esperados

Agora construa a tabela de dados esperados (tabela ideal). Para fazer isso:

• Copie os dados da coluna 1 e 6 da Tabela Real
• Copie os dados das linhas 1 e 6 da Tabela Real
• Calcule o % de cada faixa em relação ao total (última coluna)
• Distribua os valores para cada segmento de acordo com a proporção calculada (Ex: Saúde na faixa <=8% é calculado através da multiplicação entre 2 (última linha) e 0,25 (última coluna).

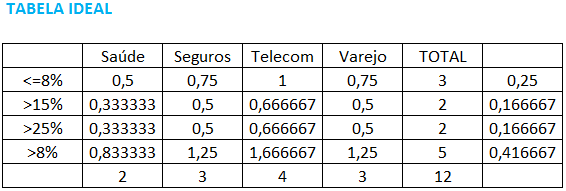
Caso queira olhar os cálculos com mais detalhes, baixe aqui a planilha de exemplo.

Passo 5 – Realizando o teste

Com as hipóteses definidas e as tabelas montadas, basta seguir os passos abaixo:

• Componha as hipóteses nos moldes: H0 não há influência e H1 há influência
• Defina o p-value, que é referente a margem de erro aceitável, o valor padrão é 5%
• Aplique a fórmula do Qui Quadrado, conforme a figura
• Verifique se o campo [Teste QuiQua] < [p-Value]
• Se o campo [T1 é] for verdadeiro, então rejeita-se a H0. Se for falso, aceita-se H0.

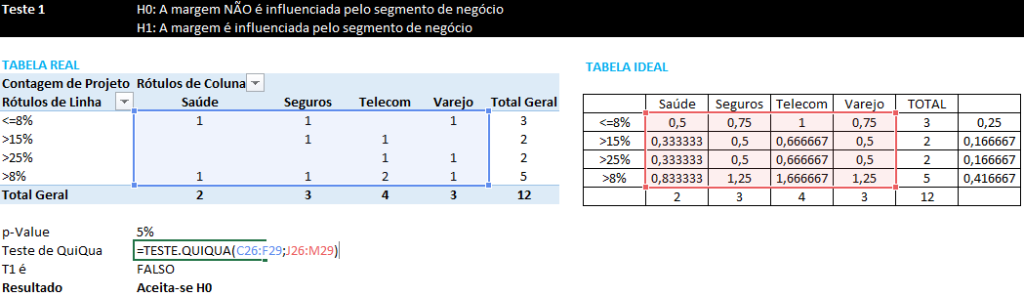
No estatística, sempre se usa a nomenclatura “Rejeita-se” ou “Aceita-se” H0. No final das contas, o que vale é o sentido. Se H0 for aceita, a hipótese nula foi aceita. Se H0 for rejeitada, a H1 é que vale.

Conclusões

No exemplo utilizado, em todos os testes aceitou-se H0. Isso era esperado, pois os dados foram aleatórios e, por isso, naturalmente não existe

Se você sobreviveu até aqui, deve ter compreendido o quanto o teste de χ² (Qui Quadrado) é útil em qualquer âmbito de trabalho e está apto a utilizá-lo para testes de hipóteses em diversas situações.

Tentei ser o mais didático possível, mas acredito que a melhor forma de aprender realmente é olhando a planilha de exemplo, por isso, a disponibilizo para download.

Agradecimentos aos professores José Dias Curto (Instituto Universitário de Lisboa) e Frederico Pereira (WABCO) que me ensinaram a usar essa poderosa ferramenta.

Espero ter ajudado!

Eli Rodrigues

 

Referências:

• http://www.somatematica.com.br/estat/ap24.php
• https://pt.wikipedia.org/wiki/Qui-quadrado
• http://www.somatematica.com.br/estat/ap28.php
• https://www.eecis.udel.edu/~portnoi/classroom/prob_estatistica/2006_1/lecture_slides/aula04.pdf